ما هي خوارزميات الحاسوب وكيف تعمل؟

ما لم تكن مهتمًا بالرياضيات أو البرمجة ، فقد تكون كلمة "خوارزمية" يونانية بالنسبة لك ، ولكنها إحدى اللبنات الأساسية لكل ما تستخدمه لقراءة هذا المقال. إليك شرح سريع لما هي عليه وكيف تعمل.

إخلاء المسؤولية: أنا لست مدرسًا للرياضيات أو علوم الكمبيوتر ، لذلك ليست كل المصطلحات التي أستخدمها تقنية. هذا لأنني أحاول شرح كل شيء بلغة إنجليزية بسيطة لأن الناس غير مرتاحين تمامًا للرياضيات. ومع ذلك ، هناك بعض الرياضيات المتضمنة ، وهذا أمر لا مفر منه. مهووسو الرياضيات ، لا تتردد في التصحيح أو الشرح بشكل أفضل في التعليقات ، ولكن من فضلك ، اجعل الأمر بسيطًا لمن لا يميلون رياضيًا بيننا.

الصورة عن طريق إيان روتسالا

ما هي الخوارزمية؟

كلمة "خوارزمية" لها أصل مشابه لـ "الجبر" ، باستثناء أن هذا يشير إلى عالم الرياضيات العربي نفسه ، الخوارزمي (مجرد معلومة مثيرة للاهتمام). الخوارزمية ، لغير المبرمجين بيننا ، هي مجموعة من التعليمات التي تأخذ مُدخلاً ، A ، وتوفر مخرجات ، B ، التي تغير البيانات المتضمنة بطريقة ما. الخوارزميات لديها مجموعة متنوعة من التطبيقات. في الرياضيات ، يمكنهم المساعدة في حساب الوظائف من النقاط في مجموعة البيانات ، من بين أشياء أكثر تقدمًا. بصرف النظر عن استخدامها في البرمجة نفسها ، فإنها تلعب أدوارًا رئيسية في أشياء مثل ضغط الملفات وتشفير البيانات.

مجموعة أساسية من التعليمات

لنفترض أن صديقك يقابلك في محل بقالة وأنك توجهه نحوك. أنت تقول أشياء مثل "تعال من خلال الأبواب اليمنى" ، "مرر قسم الأسماك على اليسار" ، و "إذا رأيت مصنع الألبان ، فقد تجاوزتني." الخوارزميات تعمل من هذا القبيل. يمكننا استخدام مخطط انسيابي لتوضيح التعليمات بناءً على المعايير التي نعرفها مسبقًا أو اكتشافها أثناء العملية.

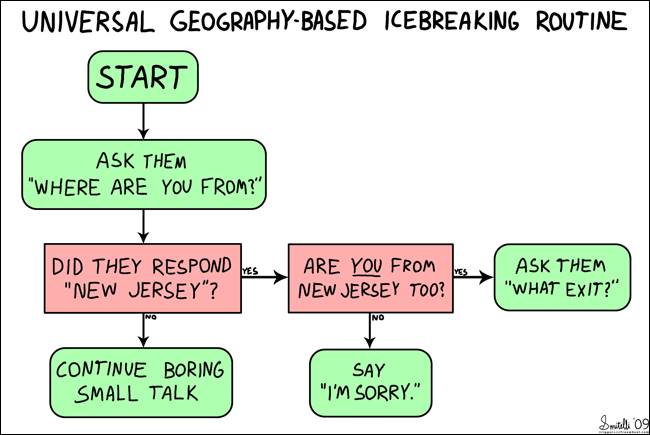
(الصورة بعنوان "Icebreaking Routine" EDIT: بإذن من Trigger and Freewheel)

من START ، ستتجه إلى المسار ، واعتمادًا على ما يحدث ، تتبع "التدفق" إلى النتيجة النهائية. المخططات الانسيابية هي أدوات مرئية يمكن أن تمثل بشكل مفهوم مجموعة من الإرشادات التي تستخدمها أجهزة الكمبيوتر. وبالمثل ، تساعد الخوارزميات في فعل الشيء نفسه مع المزيد من النماذج القائمة على الرياضيات.

الرسوم البيانية

دعنا نستخدم الرسم البياني لتوضيح الطرق المختلفة التي يمكننا بها إعطاء التوجيهات.

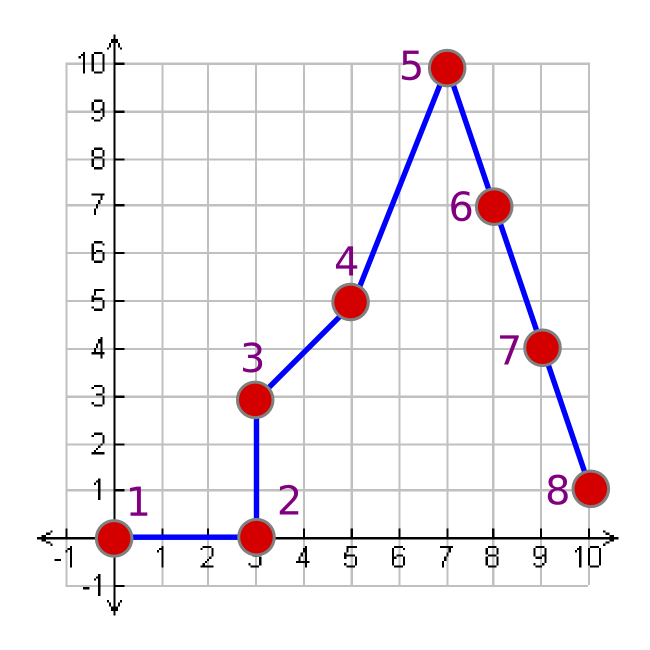
يمكننا التعبير عن هذا الرسم البياني كحلقة وصل بين جميع نقاطه. لإعادة إنتاج هذه الصورة ، يمكننا إعطاء مجموعة من التعليمات لشخص آخر.

طريقة 1

يمكننا تمثيل هذا كسلسلة من النقاط ، وستتبع المعلومات الشكل القياسي للرسم البياني = {(x1 ، y1) ، (x2 ، y2) ، ... ، (xn ، yn)}.

الرسم البياني = {(0،0)، (3،0)، (3،3)، (5،5)، (7،10)، (8،7)، (9،4)، (10،1) }

من السهل جدًا رسم كل نقطة ، واحدة تلو الأخرى ، وربطها بالنقطة السابقة. ومع ذلك ، تخيل رسمًا بيانيًا بألف نقطة أو أجزاء متعددة تسير في كل اتجاه. ستحتوي هذه القائمة على الكثير من البيانات ، أليس كذلك؟ وبعد ذلك ، قد يكون الاضطرار إلى توصيل كل واحد ، واحدًا تلو الآخر ، أمرًا مؤلمًا.

الطريقة الثانية

شيء آخر يمكننا القيام به هو إعطاء نقطة البداية ، ميل الخط الفاصل بينها وبين النقطة التالية ، وبيان مكان توقع النقطة التالية باستخدام الشكل القياسي للرسم البياني = {(نقطة البداية} ، [m1 ، x1 ، h1 ] ، ... ، [mn ، xn ، hn]}. هنا ، يمثل المتغير "m" ميل الخط ، ويمثل "x" اتجاه العد (سواء كان x أو y) ، و "h" يخبرك كيف يمكنك الاعتماد على الكثير في الاتجاه المذكور. يمكنك أيضًا تذكر رسم نقطة بعد كل حركة.

الرسم البياني = {(0،0)، [0، x، 3]، [0، y، 3]، [1، x، 2]، [2.5، x، 2]، [-3، x، 1]، [-3 ، س ، 1] ، [-3 ، س ، 1]}

ستنتهي بنفس الرسم البياني. يمكنك أن ترى أن المصطلحات الثلاثة الأخيرة في هذا التعبير هي نفسها ، لذلك قد نتمكن من تقليصها بمجرد قول "كرر ذلك ثلاث مرات" بطريقة ما. لنفترض أنه في أي وقت يظهر فيه المتغير "R" ، فهذا يعني تكرار آخر شيء. نستطيع فعل ذلك:

الرسم البياني = {(0،0)، [0، x، 3]، [0، y، 3]، [1، x، 2]، [2.5، x، 2]، [-3، x، 1]، [R = 2]}

ماذا لو لم تكن النقاط الفردية مهمة حقًا ، وفقط الرسم البياني نفسه مهم؟ يمكننا دمج الأقسام الثلاثة الأخيرة على النحو التالي:

الرسم البياني = {(0،0)، [0، x، 3]، [0، y، 3]، [1، x، 2]، [2.5، x، 2]، [-3، x، 3]}

إنه يقصر الأشياء قليلاً مما كانت عليه من قبل.

الطريقة الثالثة

دعونا نحاول القيام بهذا بطريقة أخرى.

ص = 0 ، 0≤x≤3
س = 0 ، 0≤y≤3
ص = س ، 3≤x≤5
ص = 2.5x-7.5 ، 5≤x≤7
ص = -3 س + 29 ، 7 س8
ص = -3 س + 29 ، 8≤ س≤9
ص = -3 س + 29 ، 9 × × 10

هنا لدينا من الناحية الجبرية البحتة. مرة أخرى ، إذا كانت النقاط نفسها غير مهمة وكان الرسم البياني فقط مهمًا ، فيمكننا دمج العناصر الثلاثة الأخيرة.

ص = 0 ، 0≤x≤3
س = 0 ، 0≤y≤3
ص = س ، 3≤x≤5
ص = 2.5x-7.5 ، 5≤x≤7
ص = -3 س + 29 ، 7 × × 10

الآن ، الطريقة التي تختارها تعتمد على قدراتك. ربما تكون رائعًا في الرياضيات والرسوم البيانية ، لذلك تختار الخيار الأخير. ربما تكون جيدًا في التنقل ، لذلك تختار الخيار الثاني. ومع ذلك ، في عالم الكمبيوتر ، تقوم بالعديد من أنواع المهام المختلفة وقدرة الكمبيوتر لا تتغير حقًا. لذلك ، تم تحسين الخوارزميات للمهام التي يكملونها.

نقطة أخرى مهمة يجب ملاحظتها هي أن كل طريقة تعتمد على مفتاح. كل مجموعة من التعليمات غير مجدية إلا إذا كنت تعرف ماذا تفعل بها. إذا كنت لا تعرف أنه من المفترض أن تقوم برسم كل نقطة وتوصيل النقاط ، فإن المجموعة الأولى من النقاط لا تعني شيئًا. ما لم تكن تعرف ما يعنيه كل متغير في الطريقة الثانية ، فلن تعرف كيفية تطبيقه ، تمامًا مثل مفتاح التشفير. يعد هذا المفتاح أيضًا جزءًا لا يتجزأ من استخدام الخوارزميات ، وغالبًا ما يتم العثور على هذا المفتاح في المجتمع أو عبر "معيار".

ضغط الملفات

عندما تقوم بتنزيل ملف .zip ، فإنك تستخرج المحتويات بحيث يمكنك استخدام كل ما بداخله. في الوقت الحاضر ، يمكن لمعظم أنظمة التشغيل الغوص في ملفات .zip كما لو كانت مجلدات عادية ، وتقوم بكل شيء في الخلفية. على جهاز Windows 95 الخاص بي منذ أكثر من عقد من الزمان ، كان علي استخراج كل شيء يدويًا قبل أن أرى أي شيء أكثر من أسماء الملفات بالداخل. هذا لأن ما تم تخزينه على القرص كملف .zip لم يكن في شكل قابل للاستخدام. فكر في أريكة قابلة للطي. عندما تريد استخدامه كسرير ، عليك إزالة الوسائد وفتحها ، الأمر الذي يشغل مساحة أكبر. عندما لا تحتاجها ، أو تريد نقلها ، يمكنك طيها احتياطيًا.

يتم تعديل خوارزميات الضغط وتحسينها خصيصًا لأنواع الملفات المستهدفة. تنسيقات الصوت ، على سبيل المثال ، تستخدم كل منها طريقة مختلفة لتخزين البيانات التي ، عند فك تشفيرها بواسطة برنامج ترميز الصوت ، ستعطي ملفًا صوتيًا مشابهًا لشكل الموجة الأصلي. لمزيد من المعلومات حول هذه الاختلافات ، راجع مقالتنا السابقة ، ما هي الاختلافات بين كل تلك التنسيقات الصوتية؟ تشترك تنسيقات الصوت غير المفقودة وملفات .zip في شيء واحد: كلاهما ينتج البيانات الأصلية في شكلها الدقيق بعد عملية فك الضغط. تستخدم برامج ترميز الصوت المفقودة وسائل أخرى لتوفير مساحة القرص ، مثل قطع الترددات التي لا يمكن أن تسمعها آذان الإنسان وتنعيم شكل الموجة في الأقسام للتخلص من بعض التفاصيل. في النهاية ، على الرغم من أننا قد لا نكون قادرين على سماع الفرق بين مسار MP3 ومسار CD ، إلا أن هناك بالتأكيد نقصًا في المعلومات في المسار الأول.

تشفير البيانات

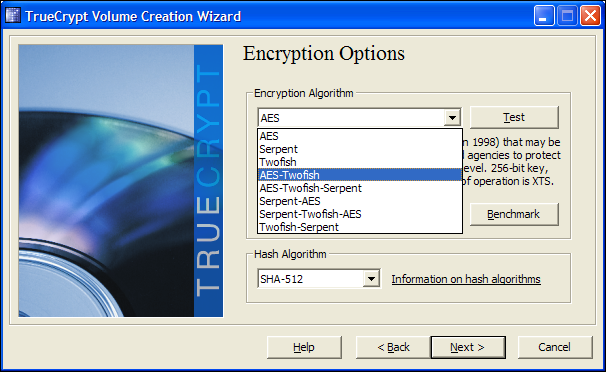
تُستخدم الخوارزميات أيضًا عند تأمين البيانات أو خطوط الاتصال. بدلاً من تخزين البيانات بحيث تستخدم مساحة أقل على القرص ، يتم تخزينها بطريقة لا يمكن اكتشافها بواسطة البرامج الأخرى. إذا قام شخص ما بسرقة محرك الأقراص الثابتة الخاص بك وبدأ في مسحه ضوئيًا ، فيمكنه التقاط البيانات حتى عند حذف الملفات لأن البيانات نفسها لا تزال موجودة ، على الرغم من اختفاء موقع إعادة التوجيه إليها. عندما يتم تشفير البيانات ، فإن كل ما يتم تخزينه لا يبدو كما هو. عادة ما يبدو عشوائيًا ، كما لو أن التجزئة قد تراكمت بمرور الوقت. يمكنك أيضًا تخزين البيانات وجعلها تظهر كنوع آخر من الملفات. تعد ملفات الصور وملفات الموسيقى مفيدة لهذا ، حيث يمكن أن تكون كبيرة جدًا دون إثارة الشك ، على سبيل المثال. يتم كل هذا باستخدام خوارزميات رياضية ، والتي تأخذ نوعًا من المدخلات وتحولها إلى نوع آخر محدد جدًا من المخرجات. لمزيد من المعلومات حول كيفية عمل التشفير ، تحقق من HTG يوضح: ما هو التشفير وكيف يعمل؟

الخوارزميات هي أدوات رياضية توفر مجموعة متنوعة من الاستخدامات في علوم الكمبيوتر. إنهم يعملون على توفير مسار بين نقطة البداية ونقطة النهاية بطريقة متسقة ، ويقدمون الإرشادات لاتباعها. تعرف أكثر مما أبرزناه؟ شارك شروحاتك في التعليقات!