Que sont les algorithmes informatiques et comment fonctionnent-ils ?

À moins que vous ne soyez amateur de mathématiques ou de programmation, le mot « algorithme » pourrait être grec pour vous, mais c'est l'un des éléments constitutifs de tout ce que vous utilisez pour lire cet article. Voici une explication rapide de ce qu'ils sont et de leur fonctionnement.

Avis de non-responsabilité : je ne suis pas professeur de mathématiques ou d'informatique, donc tous les termes que j'utilise ne sont pas techniques. C'est parce que j'essaie de tout expliquer en anglais simple car les gens ne sont pas très à l'aise avec les mathématiques. Cela étant dit, il y a des mathématiques impliquées, et c'est inévitable. Les geeks des mathématiques, n'hésitez pas à corriger ou mieux expliquer dans les commentaires, mais s'il vous plaît, restez simple pour ceux qui ne sont pas enclins aux mathématiques parmi nous.

Image par Ian Ruotsala

Qu'est-ce qu'un algorithme ?

Le mot « algorithme » a une étymologie similaire à « algèbre », sauf qu'il fait référence au mathématicien arabe lui-même, al-Khwarizmi (juste une friandise intéressante). Un algorithme, pour les non-programmeurs parmi nous, est un ensemble d'instructions qui prennent une entrée, A, et fournissent une sortie, B, qui modifie les données impliquées d'une manière ou d'une autre. Les algorithmes ont une grande variété d'applications. En mathématiques, ils peuvent aider à calculer des fonctions à partir de points dans un ensemble de données, parmi des choses beaucoup plus avancées. Outre leur utilisation dans la programmation elle-même, ils jouent un rôle majeur dans des choses comme la compression de fichiers et le cryptage des données.

Un ensemble d'instructions de base

Disons que votre ami vous rencontre dans une épicerie et que vous le guidez vers vous. Vous dites des choses comme "entrez par les portes de droite", "passez la section des poissons sur la gauche" et "si vous voyez la laiterie, vous m'avez dépassé". Les algorithmes fonctionnent comme ça. Nous pouvons utiliser un organigramme pour illustrer des instructions basées sur des critères que nous connaissons à l'avance ou que nous découvrons au cours du processus.

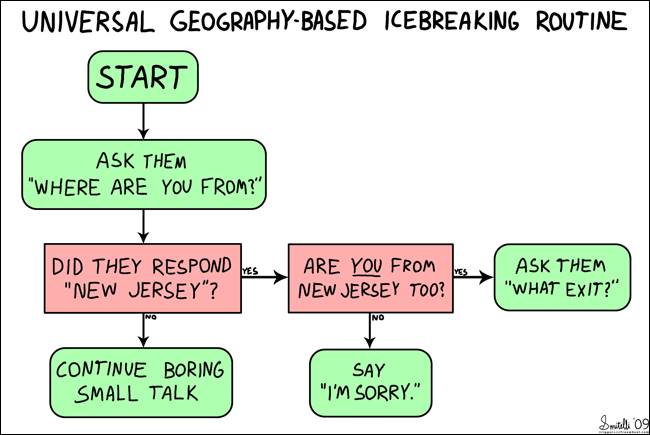
(image intitulée "Icebreaking Routine" EDIT : avec l'aimable autorisation de Trigger et Freewheel)

À partir de START, vous emprunterez le chemin et, en fonction de ce qui se passe, vous suivrez le «flux» jusqu'au résultat final. Les organigrammes sont des outils visuels qui peuvent représenter de manière plus compréhensible un ensemble d'instructions utilisées par les ordinateurs. De même, les algorithmes aident à faire de même avec des modèles plus mathématiques.

Graphiques

Utilisons un graphique pour illustrer les différentes façons dont nous pouvons donner des directions.

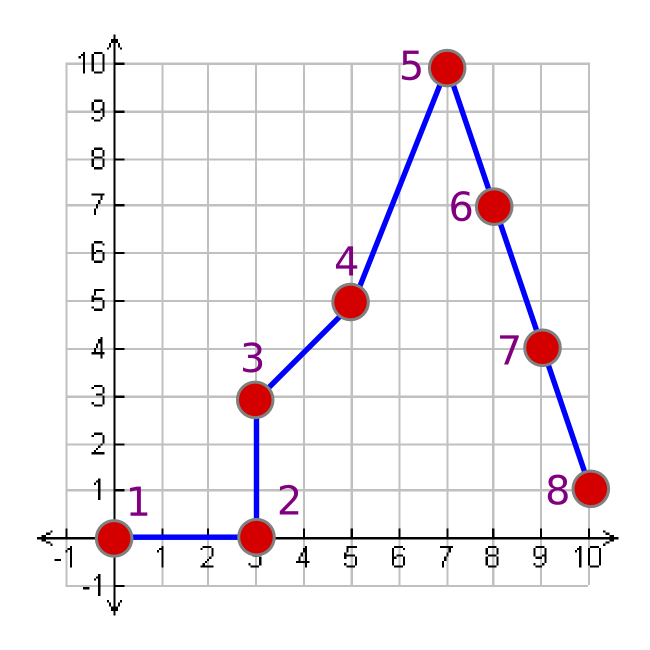
Nous pouvons exprimer ce graphique comme une connexion entre tous ses points. Afin de reproduire cette image, nous pouvons donner un ensemble d'instructions à quelqu'un d'autre.

Méthode 1

Nous pouvons représenter cela comme une série de points, et les informations suivraient la forme standard du graphique = {(x1, y1), (x2, y2), …, (xn, yn)}.

graphique = {(0,0), (3,0), (3,3), (5,5), (7,10), (8,7), (9,4), (10,1) }

Il est assez facile de tracer chaque point, l'un après l'autre, et de les relier au point précédent. Cependant, imaginez un graphique avec mille points ou plusieurs segments allant tous dans tous les sens. Cette liste contiendrait beaucoup de données, n'est-ce pas ? Et puis devoir connecter chacun, un à la fois, peut être pénible.

Méthode 2

Une autre chose que nous pouvons faire est de donner un point de départ, la pente de la ligne entre celui-ci et le point suivant, et d'indiquer où attendre le point suivant en utilisant la forme standard de graph={(starting point}, [m1, x1, h1 ], …, [mn, xn, hn]}. Ici, la variable 'm' représente la pente de la droite, 'x' représente la direction dans laquelle compter (que ce soit x ou y), et 'h' vous indique comment plusieurs à compter dans ladite direction. Vous pouvez également vous rappeler de tracer un point après chaque mouvement.

graphique = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,1], [-3,x,1], [-3,x,1]}

Vous vous retrouverez avec le même graphique. Vous pouvez voir que les trois derniers termes de cette expression sont les mêmes, nous pouvons donc peut-être réduire cela en disant simplement "répétez cela trois fois" d'une manière ou d'une autre. Disons que chaque fois que vous voyez la variable 'R' apparaître, cela signifie répéter la dernière chose. Nous pouvons le faire:

graphique = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,1], [R=2]}

Que se passe-t-il si les points individuels n'ont pas vraiment d'importance, et que seul le graphique lui-même compte ? Nous pouvons consolider ces trois dernières sections comme suit :

graphique = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,3]}

Cela raccourcit un peu les choses par rapport à ce qu'elles étaient auparavant.

Méthode 3

Essayons de faire cela d'une autre manière.

y=0, 0≤x≤3
x=0, 0≤y≤3
y=x, 3≤x≤5
y=2.5x-7.5, 5≤x≤7
y=-3x+29, 7≤x≤8
y=-3x+29, 8≤x≤9
y=-3x+29, 9≤x≤10

Ici, nous l'avons en termes algébriques purs. Encore une fois, si les points eux-mêmes n'ont pas d'importance et que seul le graphique en a, nous pouvons consolider les trois derniers éléments.

y=0, 0≤x≤3
x=0, 0≤y≤3
y=x, 3≤x≤5
y=2.5x-7.5, 5≤x≤7
y=-3x+29, 7≤x≤10

Maintenant, la méthode que vous choisissez dépend de vos capacités. Peut-être que vous êtes doué pour les mathématiques et les graphiques, alors vous choisissez la dernière option. Peut-être que vous êtes doué pour la navigation, alors vous choisissez la deuxième option. Dans le domaine des ordinateurs, cependant, vous effectuez de nombreux types de tâches différentes et la capacité de l'ordinateur ne change pas vraiment. Par conséquent, les algorithmes sont optimisés pour les tâches qu'ils accomplissent.

Un autre point important à noter est que chaque méthode repose sur une clé. Chaque ensemble d'instructions est inutile à moins que vous ne sachiez quoi en faire. Si vous ne savez pas que vous êtes censé tracer chaque point et relier les points, le premier ensemble de points ne signifie rien. À moins que vous ne sachiez ce que chaque variable signifie dans la deuxième méthode, vous ne saurez pas comment les appliquer, un peu comme la clé d'un chiffrement. Cette clé fait également partie intégrante de l'utilisation des algorithmes, et souvent, cette clé se trouve dans la communauté ou via une « norme ».

Compression de fichiers

Lorsque vous téléchargez un fichier .zip, vous en extrayez le contenu afin de pouvoir utiliser tout ce qu'il contient. De nos jours, la plupart des systèmes d'exploitation peuvent plonger dans les fichiers .zip comme s'il s'agissait de dossiers normaux, faisant tout en arrière-plan. Sur ma machine Windows 95 il y a plus de dix ans, j'ai dû tout extraire manuellement avant de pouvoir voir autre chose que les noms de fichiers à l'intérieur. C'est parce que ce qui était stocké sur le disque sous forme de fichier .zip n'était pas sous une forme utilisable. Pensez à un canapé-lit. Lorsque vous souhaitez l'utiliser comme lit, vous devez retirer les coussins et le déplier, ce qui prend plus de place. Lorsque vous n'en avez pas besoin ou que vous souhaitez le transporter, vous pouvez le replier.

Les algorithmes de compression sont ajustés et optimisés spécifiquement pour les types de fichiers auxquels ils sont destinés. Les formats audio, par exemple, utilisent chacun une manière différente de stocker les données qui, une fois décodées par le codec audio, donneront un fichier son similaire à la forme d'onde d'origine. Pour plus d'informations sur ces différences, consultez notre article précédent, Quelles sont les différences entre tous ces formats audio ? Les formats audio sans perte et les fichiers .zip ont une chose en commun : ils fournissent tous les deux les données d'origine dans leur forme exacte après le processus de décompression. Les codecs audio avec perte utilisent d'autres moyens pour économiser de l'espace disque, tels que la réduction des fréquences qui ne peuvent pas être entendues par les oreilles humaines et le lissage de la forme d'onde dans les sections pour se débarrasser de certains détails. En fin de compte, même si nous ne pouvons pas vraiment entendre la différence entre une piste MP3 et une piste CD, il y a certainement un déficit d'informations dans le premier.

Cryptage des données

Les algorithmes sont également utilisés lors de la sécurisation des données ou des lignes de communication. Au lieu de stocker des données de manière à utiliser moins d'espace disque, elles sont stockées d'une manière indétectable par d'autres programmes. Si quelqu'un vole votre disque dur et commence à l'analyser, il peut récupérer des données même lorsque vous supprimez des fichiers, car les données elles-mêmes sont toujours là, même si l'emplacement de transfert vers celui-ci a disparu. Lorsque les données sont cryptées, tout ce qui est stocké ne ressemble pas à ce qu'il est. Cela semble généralement aléatoire, comme si la fragmentation s'était accumulée au fil du temps. Vous pouvez également stocker des données et les faire apparaître comme un autre type de fichier. Les fichiers image et les fichiers musicaux sont bons pour cela, car ils peuvent être assez volumineux sans éveiller les soupçons, par exemple. Tout cela est fait en utilisant des algorithmes mathématiques, qui prennent une sorte d'entrée et la convertissent en un autre type de sortie très spécifique. Pour plus d'informations sur le fonctionnement du chiffrement, consultez HTG explique : Qu'est-ce que le chiffrement et comment ça marche ?

Les algorithmes sont des outils mathématiques qui offrent une variété d'utilisations en informatique. Ils travaillent pour fournir un chemin entre un point de départ et un point final de manière cohérente, et fournissent les instructions pour le suivre. En savoir plus que ce que nous avons mis en évidence ? Partagez vos explications dans les commentaires !